https://www.acmicpc.net/problem/2581
문제
자연수 M과 N이 주어질 때 M이상 N이하의 자연수 중 소수인 것을 모두 골라 이들 소수의 합과 최솟값을 찾는 프로그램을 작성하시오.
예를 들어 M=60, N=100인 경우 60이상 100이하의 자연수 중 소수는 61, 67, 71, 73, 79, 83, 89, 97 총 8개가 있으므로, 이들 소수의 합은 620이고, 최솟값은 61이 된다.
입력
입력의 첫째 줄에 M이, 둘째 줄에 N이 주어진다.
M과 N은 10,000이하의 자연수이며, M은 N보다 작거나 같다.
출력
M이상 N이하의 자연수 중 소수인 것을 모두 찾아 첫째 줄에 그 합을, 둘째 줄에 그 중 최솟값을 출력한다.
단, M이상 N이하의 자연수 중 소수가 없을 경우는 첫째 줄에 -1을 출력한다.
해설 및 생각
문제는 단순하게 범위가 주어지면 그 사이의 소수를 구하고 그 소수들의 합과 최솟값을 출력하면 되는 문제이다.
그래서 나는 소수 판별을 위해 bool값을 설정하고 소수 정의에 따른 풀이를 써내려갔다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int M = sc.nextInt();
int N = sc.nextInt();
int minNum = Integer.MAX_VALUE;
int sum = 0;
boolean foundPrime = false;
for (int i = M; i <= N ; i++) {
if (i < 2) continue; // 1은 소수가 아님
boolean isPrimeNumber = true;
for (int j = 2; j <= Math.sqrt(i); j++) {
if(i % j == 0) {
isPrimeNumber = false;
break;
}
}
if(isPrimeNumber) {
sum += i;
if(i < minNum) minNum = i;
foundPrime = true;
}
}
if(!foundPrime){
System.out.println(-1);
} else {
System.out.println(sum);
System.out.println(minNum);
}
}
}
하지만 소수를 판별 하는 거면 위와같이 소수의 정의에 따라 bool값으로 구분해도 괜찮겠지만 이 풀이는 특정 범위의 소수를 개별적으로 판별하기 때문에 거진 N^2의 시간복잡도를 가진다. 따라서 N의 값이 크다면 에라토스테네스의 체를 사용하는 것을 추천한다! 결론 부터 말하자면 해당 알고리즘을 이용하면

와 같은 거진 n과 같은 선형적인 시간 복잡도를 가진다. 에라토스테네스의 체 사용 시: O(N log log N) – > 전체 범위의 소수를 미리 구해놓고, 구간별 소수 합을 빠르게 처리 가능하기 때문에 굉장히 빠르다!
이 알고리즘의 원리는 간단하게 판별하고자 하는 수(해당수라 하겠다) 가 소수라면 해당수의 배수들은 모두 해당수를 약수로 가지고 있으므로 소수가 되지 못한다는 원리이다.
정리하자면,
1)지워지지 않는 가장 작은 수를 찾는다.(보통 2부터 시작)
2)해당 수는 소수이다.
3)해당수의 배수들을 모두 지운다.
예를 들어 설명해보겠다.
N=100일때 1~100사이의 소수를 구해보자
1은 예외이므로 제외하고 시작한다.
먼저, 지워지지 않는 가장 작은수는 2이고, 2의 배수들을 다 삭제한다(검은글자는 소수거나 지워지지 않은 수, 회색글자는 지워진 수)
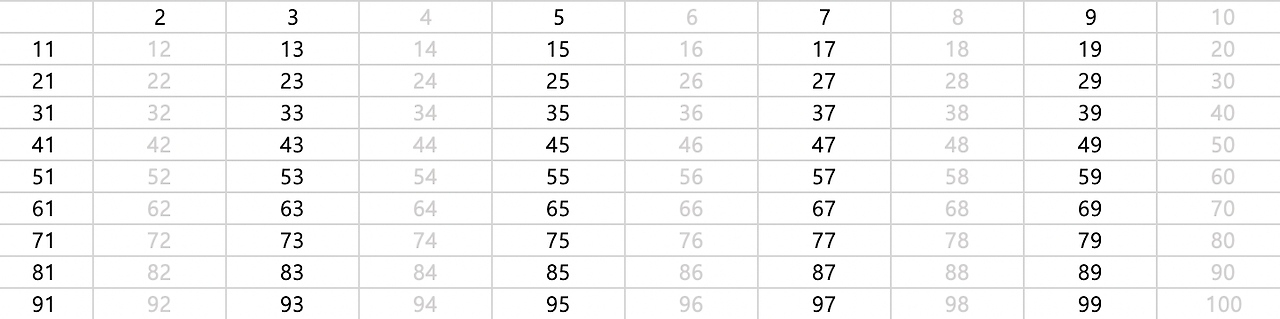
그 다음 지워지지 않는 가장 작은수는 3이고, 3의 배수들을 다 삭제한다.
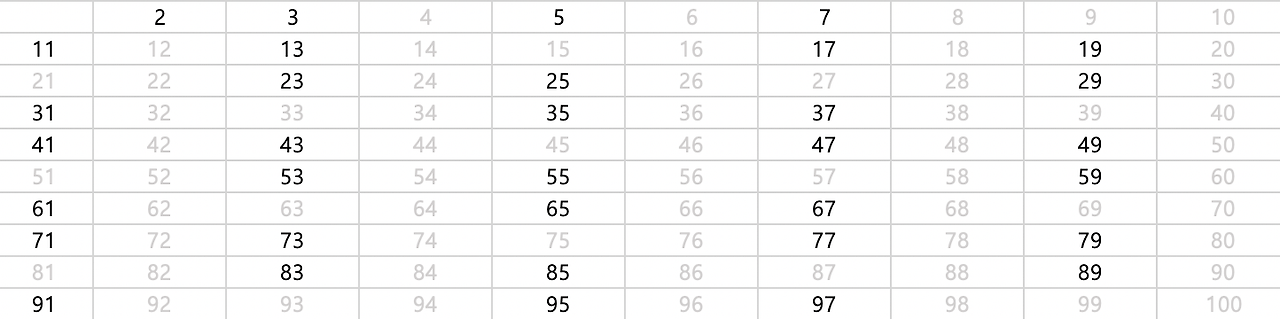
그 다음 지워지지 않는 가장 작은수는 5이고, 5의 배수들을 다 삭제한다.

그러면 짜잔~ 소수만 남게된다. 이렇게 소수를 미리 싹 다 구해놓고 여기서 최소 최대를 구하던~ 합을 구하던 하는거다! 미리 구해놓고 하기때문에 시간복잡도가 선형에 가까워 지지 않겠는가!
다시 돌아와서 위의 문제를 에라토스테네스의 체를 이용하여 풀어보겠다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int A[] = new int[10001];
for(int i=2; i<10001; i++){
A[i] = i;
}
for (int i = 2; i < Math.sqrt(10001); i++) {
if(A[i] == i){
for (int j = i+i; j <10001 ; j= j+i) {
A[j] =0;
}
}
}
int M = sc.nextInt();
int N = sc.nextInt();
int sum = 0;
int min = 0;
for (int i = N; i >=M; i--) {
sum += A[i];
if(A[i] != 0){
min = A[i];
}
}
if(sum == 0){
System.out.println(-1);
}else{
System.out.println(sum);
System.out.println(min);
}
}
}
이렇게 위에서 미리 소수의 배수들을 지워서 소수를 구해놓고 아래서 최소와 합을 구했다.
여기서 소수판별 범위도 어떤 수 N이 소수가 아니면, 그 약수는 반드시 √N 이하에 존재하기 때문에 범위를 ; i < Math.sqrt(10001); 이렇게 해주어 체의 효율을 더 높혔다!
소수 판별 관련 문제는 알고리즘이나 코테에서 자주 나온다고 하니 확실하게 알아놓자!
'Problem Solve' 카테고리의 다른 글
| [JAVA] 1629번-곱셈 🩶1, 4375번-1 🩶3 : 자료형의 범위를 벗어나는 상황에서는 모듈러 연산의 특징을 이용하자. (정수론) (0) | 2026.02.01 |
|---|---|
| [JAVA] 11286번 절댓값 힙 🩶1 : 시간초과...💥 우선순위 큐(Priority Queue)가 뭔데..? (1) | 2026.01.21 |
| [JAVA] 2231번 분해합 🤎2 : 구현만 하면 되는데...! 😂 (9) | 2024.11.14 |
| [JAVA] 2798번 블랙잭 🤎2 : 나의 첫 무서운 브루트포스 알고리즘 풀이 (2) | 2024.11.13 |
| [JAVA] 백준 1978번 소수찾기 🤎2 : 소수의 약수 범위에 대한 매우 중요한 생각! (0) | 2024.11.11 |